Desktop-Bild

Projekt: Branch- and Bound Algorithmen für das equitable Graphenfärbungsproblem

Förderung: DFG Exellence Initiative
Lehrstuhl II für Mathematik, Lehr- und Forschungsgebiet Diskrete Optimierung
RWTH Aachen University
Overview / The equitable coloring problem / Code and Data /

The equitable coloring problem


Graph coloring

Given an undirected graph G=(V,E), the graph coloring problem asks for

Applications:


What about 'fairness'?

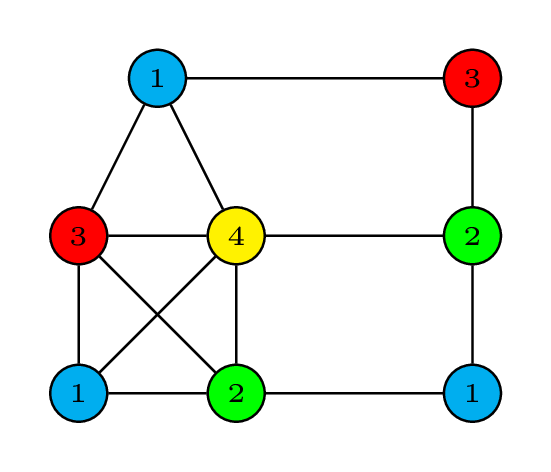
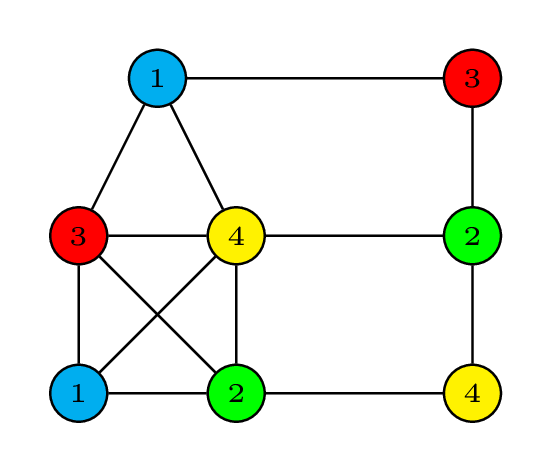
standardColoring equitableColoring
Fig.1 - 'normal' vs. equitable colorings

Equitable coloring

We consider an extension of the graph coloring problem. We ask whether there is a coloring, that is a function f, with the additional properties that

Algorithmic approach: DSATUR

Enummerate all possible equitable colorings in a tree-like structure. Branching and Bounding where possible. Compare the example in Figure 2. On the left, the tree-like enummeration of the colorings, on the right, the corresponding graph coloring.
Gif
Fig.2 - DSATUR for equitable colorings
last modified: 10/09/2016 - 16:03